Jumat, 12 April 2013

MATEMATIKA EKONOMI II ( PENGERTIAN DAN JENIS MATRIKS )

Matriks adalah kumpulan bilangan berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Pemanfaatannya misalnya dalam menjelaskan persamaan linier, transformasi koordinat, dan lainnya. Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan.








Penjumlahan dan pengurangan matriks hanya dapat dilakukan apabila kedua matriks memiliki ukuran atau tipe yang sama. Elemen-elemen yang dijumlahkan atau dikurangi adalah elemen yang posisi atau letaknya sama.
 
 

atau dalam representasi dekoratfinya








Perkalian Skalar

Matriks dapat dikalikan dengan sebuah skalar.
\lambda\cdot A := (\lambda\cdot a_{ij})_{i=1, \ldots , m; \ j=1, \ldots , n}
Contoh perhitungan :
5 \cdot \begin{pmatrix} 1 & -3 & 2 \\ 1 & 2 & 7 \end{pmatrix} = \begin{pmatrix} 5 \cdot 1 & 5 \cdot (-3) & 5 \cdot 2 \\ 5 \cdot 1 & 5 \cdot 2 & 5 \cdot 7 \end{pmatrix} = \begin{pmatrix} 5 & -15 & 10 \\ 5 & 10 & 35 \end{pmatrix}

Matriks dapat dikalikan, dengan cara tiap baris dikalikan dengan tiap kolom, lalu dijumlahkan pada baris yang sama.

c_{ij}=\sum_{k=1}^m a_{ik}\cdot b_{kj}
Contoh perhitungan :
\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{pmatrix} \cdot \begin{pmatrix} 6 & -1 \\ 3 & 2 \\ 0 & -3 \end{pmatrix} = \begin{pmatrix} 1 \cdot 6 + 2 \cdot 3 + 3 \cdot 0 & 1 \cdot (-1) + 2 \cdot 2 + 3 \cdot (-3) \\ 4 \cdot 6 + 5 \cdot 3 + 6 \cdot 0 & 4 \cdot (-1) + 5 \cdot 2 + 6 \cdot (-3) \\ \end{pmatrix} = \begin{pmatrix} 12 & -6 \\ 39 & -12 \end{pmatrix}

Jenis-jenis Matriks
Jenis-jenis matriks dapat dibagi berdasarkan ordo dan elemen / unsur dari matriks tersebut.

Berdasarkan ordo Matriks dapat di bagi menjadi beberapa jenis yaitu:
  • Matriks Bujursangkar adalah matriks yang memiliki ordo n x n atau banyaknya baris sama dengan banyaknya  kolom yang terdapat dalam mtriks tersebut. Matriks ini disebut juga dengan matriks persegi berordo n.
          Contoh : 
  • Matriks Baris adalah Matriks Baris adalah matriks yang terdiri dari satu baris
          Contoh :    A =  ( 2  1  3  -7 )
  • Matriks Kolom adalah  Matriks Kolom adalah matriks yang terdiri dari satu kolom.
          Contoh :   
                            
  • Matriks Tegak  adalah  suatu matriks yang banyaknya baris lebih dari banyaknya kolom.
          Contah :
  • Matriks datar adalah Matriks  yang banyaknya baris kurang dari banyaknya kolom.
       Contoh :


Berdasarkan elemen-elemen penyusunnya matriks  dapat di bagi menjadi beberapa jenis yaitu:
  • Matriks Nol adalah Suatu matriks   yang setiap unsurnya 0 berordo  m x n, ditulis dengan huruf  O. 
        contoh :
  • Matriks Diagonal adalah  suatu matriks bujur sangkar yang  semua unsurnya , kecuali unsur-unsur pada diagonal utama adalah nol.
       Contah :  
  • Matriks Segi Tiga adalah  suatu matriks bujur sangkar yang unsur-unsur dibawah atau diatas diagonal utama semuanya 0 .

Contoh : 
       Dimana Matriks C disebut matriks segi tiga bawah dan matriks D disebut matriks segitiga atas.
  • Matriks Skalar adalah matriks diagonal yang unsur-unsur pada diagonal utama semuanya sama.
       Contoh :
  • Matriks Identitas atau Matriks Satuan adalah matriks diagonal yang unsur-unsur pada diagonal utama semuanya satu ditulis dengan huruf  I.
       Contoh :


  • Matriks Simetri adalah  suatu matriks bujur sangkar yang unsur pada baris ke-i kolom ke-j  sama dengan unsur pada baris ke-j kolom ke-i sehingga aij = aji .
       Contoh : 


Diposting oleh di
Label:

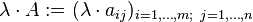
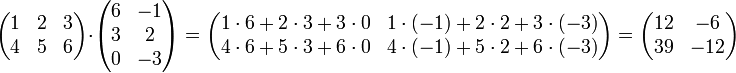
Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)